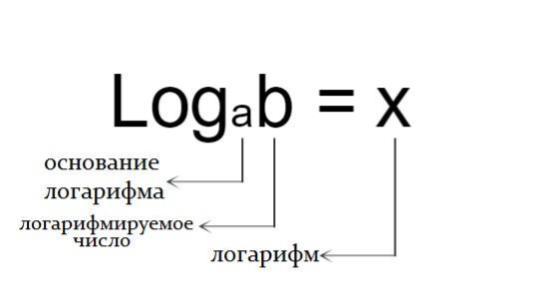Содержание материала
- Формулы и свойства логарифмов
- Видео
- Основное логарифмическое тождество
- Десятичный и натуральный логарифмы
- Интеграл
- Вычисление логарифма равносильно решению показательного уравнения
- Зачем нужны логарифмы в жизни
- Логарифм Непера или натуральный логарифм
- Свойства логарифмов
- Натуральный логарифм
- Десятичные логарифмы
- Графики логарифма
- Как число записать в виде логарифма?
Формулы и свойства логарифмов
Некоторые из основных правил логарифма:
- Когда логарифмируемое число равно основанию логарифма, логарифм всегда будет равен 1 ;
- Логарифм с любым основанием, число которого равно 1, всегда будет иметь результат равным 0 ;
- Два логарифма с одинаковым основанием всегда будут иметь одинаковые числа ;
- Если основание «а» возведено в степень логарифма с основанием «а» числа «b», то он равен «b» ;
- В случае умножения чисел мы можем превратить их в сумму двух логарифмов с одинаковыми основаниями ;
- А в случае деления чисел мы превращаем их в вычитание двух логарифмов с одинаковыми основаниями ;
- Правило возведения в степень: логарифм в степени упрощается путём умножения степени на логарифм, сохраняя её основание и число (тоже самое делается с логарифмом в квадрате)
Формулы перехода к новому основанию:
Видео
Основное логарифмическое тождество
При условии, что a > 0, a ≠ 1, b > 0 можно записать основное логарифмическое тождество
alogab = b
Примеры:3log3 7 = 7
3-log3 7 =
4log2 7 =22 log2 7 = (2log2 7)2 = 72 = 49
21 + log2 7 = 2 · 2log2 7 = 2 · 7 = 14
Десятичный и натуральный логарифмы
Как указано в определении логарифма, его основанием может быть любое положительное число, кроме единицы \((a>0, a\neq1)\). И среди всех возможных оснований есть два встречающихся настолько часто, что для логарифмов с ними придумали особую короткую запись:
То есть, \(\ln{a}\) это то же самое, что и \(\log_{e}{a}\), где \(a\) — некоторое число.
То есть, \(\lg{a}\) это то же самое, что и \(\log_{10}{a}\), где \(a\) — некоторое число.
Интеграл
Интеграл от логарифма вычисляется интегрированием по частям: \( \displaystyle \int{\log_ax\, dx}= \int{ \dfrac{\log_{\,e}x}{\log_{\,e}a} dx}= \) \( \displaystyle \dfrac1{\log_{\,e}a} \int{\log_{\,e}x\, dx}\equiv \) \( \displaystyle \frac1{\ln a} \int{\ln x\, dx}= \) \( \displaystyle \frac1{\ln a} \left( \ln x \cdot x — \int{x\, (\ln x)’\, dx} \right)= \) \( \displaystyle \frac1{\ln a} \left( \ln x \cdot x — \int{x\, \frac1x\ dx} \right)= \) \( \displaystyle \frac1{\ln a} \left( \ln x \cdot x — \int{ dx} \right)= \) \( \displaystyle \frac1{\ln a} \left( \ln x \cdot x — x \right)+C= \) \( \displaystyle \frac{x\,(\,\ln x-1)}{\ln a}+C \). Итак, \( \displaystyle \int{\log_{\,a}x\, dx}= \frac{x\,(\,\ln x-1)}{\ln a}+C \)
Вычисление логарифма равносильно решению показательного уравнения
Показательное уравнение:
ax = b,
при условии a > 0, a ≠ 1; b > 0, где
x — показатель степени, a — основа степени, b — степень числа a.
Логарифмическое уравнение:
loga b = x,
при условии a > 0, a ≠ 1; b > 0, где
x — логарифм числа b с основой a, a — основа логарифма, b — число, которое стоит под знаком логарифма.
Примеры: 25 = 32 ⇔ 5 = log2 32 34 = 81 ⇔ 4 = log3 81 log1/5 125 = -3 ⇔ (1/5)-3 = 125 log2 116 = -4 ⇔ 2-4 = 116.
Пример 1
Найти логарифм: log 4 8
Обозначим log4 8 через x:
log4 8 = x
Перейдем к показательному уравнению:
4x = 8
Сведем показательное уравнение к основе 2 и решим его:
22x = 23
2x = 3
x =
Ответ: log4 8 = 3 2
Пример 2
Найти x если : logx 125 =
За определением логарифма имеем:
x3/2 = 125
Возведем обе части в степень
(x3/2)2/3 = 1252/3
x = (53)2/3 = 53·2/3 = 52 = 25
Ответ: x = 25
Зачем нужны логарифмы в жизни
Вокруг нас и в быту мы встречаем гораздо больше логарифмов, чем кажется. Вот несколько примеров.
Децибелы, в которых измеряется относительная громкость любых звуков, считаются по десятичному логарифму. Относительная — потому что она считается от минимального порога громкости, которую только может расслышать человек. Например, если громкость звука равна 20 децибел, то это значит, что это громче самого тихого в 100 раз, а если 30 децибел — то в 1000 раз.
В химии активность водородных ионов тоже считается по логарифмической шкале.
Выдержки и диафрагмы в фотографии тоже меняются логарифмически — каждое новое значение больше или меньше предыдущего в определённое число раз.
В ракетостроении для вычисления скорости ракеты используется уравнение Циолковского. В основе этого уравнения — логарифмическая зависимость от массы ракеты с топливом и без него.
Логарифм Непера или натуральный логарифм
Состоит из логарифма, основанного на иррациональном числе, которое называется «число Эйлера», пишется как «e» и приблизительно равно 2,718281. Является обратной функцией к экспоненциальной функции.
Название логарифма («логарифм Непера») произошло от имени его изобретателя — математика Джона Непера.
Свойства логарифмов
Перечисленные ниже свойства логарифмов вытекают из основного логарифмического тождества:
 |  |
 |  |
 |  |
 |   (основное свойство логарифмов), (основное свойство логарифмов), |
 |   (основное свойство логарифмов), (основное свойство логарифмов), |
 |  |
 |  |
 |   (формула перехода к новому основанию логарифмов), (формула перехода к новому основанию логарифмов), |
 |  |
 |  |
 |
 |
 |
 (основное свойство логарифмов), (основное свойство логарифмов), |
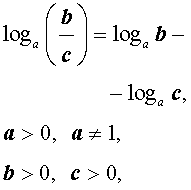 (основное свойство логарифмов), (основное свойство логарифмов), |
 |
 |
 (формула перехода к новому основанию логарифмов), (формула перехода к новому основанию логарифмов), |
 |
 |
Натуральный логарифм
Натуральным логарифмом называется логарифм по основанию \(e\). Обозначение — \(ln(x)\). Что такое \(e\)? Так обозначают экспоненту, число-константу, равную, примерно, \(2,718281828459…\). Это число известно тем, что используется в многих математических законах. Просто запомните, что логарифмы с основанием \(e\) часто встречаются, и поэтому им придумали специальное название – натуральный логарифм.
Пример 7
Натуральные и десятичные логарифмы подчиняются тем же самым свойствам и правилам, что и обыкновенные логарифмы.
У логарифмов есть несколько свойств, по которым можно проводить преобразования и вычисления. Кроме этих свойств, никаких операций с логарифмами делать нельзя.
Десятичные логарифмы
Логарифм по основанию \(\displaystyle 10\) называется десятичным логарифмом и записывается упрощенно: \(\displaystyle \lg \) вместо \(\displaystyle {{\log }_{10}}\)
Например:
- \(\displaystyle \lg 100=2\);
- \(\displaystyle \lg 1000=3\);
- \(\displaystyle \lg {{10}^{15}}=15\);
- \(\displaystyle \lg 0,1=-1\);
- \(\displaystyle \lg 0,01=-2\).
Графики логарифма

График логарифма получается из графика показательной функции зеркальным отражением относительно прямой y = x. Слева изображены графики функции y = loga x для четырех значений основания логарифма: a = 2, a = 8, a = 1/2 и a = 1/8. На графике видно, что при a > 1 логарифм монотонно возрастает. С увеличением x рост существенно замедляется. При < a < 1 логарифм монотонно убывает.
Как число записать в виде логарифма?
Как уже было сказано выше – любой логарифм это просто число. Верно и обратное: любое число может быть записано как логарифм. Например, мы знаем, что \(\log_{2}{4}\) равен двум. Тогда можно вместо двойки писать \(\log_{2}{4}\).
Но \(\log_{3}{9}\) тоже равен \(2\), значит, также можно записать \(2=\log_{3}{9}\) . Аналогично и с \(\log_{5}{25}\), и с \(\log_{9}{81}\), и т.д. То есть, получается
\(2=\log_{2}{4}=\log_{3}{9}=\log_{4}{16}=\log_{5}{25}=\log_{6}{36}=\log_{7}{49}…\)
Таким образом, если нам нужно, мы можем где угодно (хоть в уравнении, хоть в выражении, хоть в неравенстве) записывать двойку как логарифм с любым основанием – просто в качестве аргумента пишем основание в квадрате.
Точно также и с тройкой – ее можно записать как \(\log_{2}{8}\), или как \(\log_{3}{27}\), или как \(\log_{4}{64}\)… Здесь мы как аргумент пишем основание в кубе:
\(3=\log_{2}{8}=\log_{3}{27}=\log_{4}{64}=\log_{5}{125}=\log_{6}{216}=\log_{7}{343}…\)
И с четверкой:
\(4=\log_{2}{16}=\log_{3}{81}=\log_{4}{256}=\log_{5}{625}=\log_{6}{1296}=\log_{7}{2401}…\)
И с минус единицей:
\(-1=\) \(\log_{2}\)\(\frac{1}{2}\)\(=\) \(\log_{3}\)\(\frac{1}{3}\)\(=\) \(\log_{4}\)\(\frac{1}{4}\)\(=\) \(\log_{5}\)\(\frac{1}{5}\)\(=\) \(\log_{6}\)\(\frac{1}{6}\)\(=\) \(\log_{7}\)\(\frac{1}{7}\)\(…\)
И с одной третьей:
\(\frac{1}{3}\)\(=\log_{2}{\sqrt[3]{2}}=\log_{3}{\sqrt[3]{3}}=\log_{4}{\sqrt[3]{4}}=\log_{5}{\sqrt[3]{5}}=\log_{6}{\sqrt[3]{6}}=\log_{7}{\sqrt[3]{7}}…\)
И так далее.
Пример: Найдите значение выражения \(\frac{\log_{2}{14}}{1+\log_{2}{7}}\)
Решение:
| \(\frac{\log_{2}{14}}{1+\log_{2}{7}}\)\(=\) | Превращаем единицу в логарифм с основанием \(2\): \(1=\log_{2}{2}\) | |
| \(=\)\(\frac{\log_{2}{14}}{\log_{2}{2}+\log_{2}{7}}\)\(=\) | Теперь пользуемся свойством логарифмов: \(\log_{a}{b}+\log_{a}{c}=\log_{a}{(bc)}\) | |
| \(=\)\(\frac{\log_{2}{14}}{\log_{2}{(2\cdot7)}}\)\(=\)\(\frac{\log_{2}{14}}{\log_{2}{14}}\)\(=\) | В числителе и знаменателе одинаковые числа – их можно сократить. | |
| \(=1\) | Ответ готов. |
Ответ: \(1\)
Смотрите также: Логарифмические уравнения Логарифмические неравенства