Содержание материала
Что такое матрицы в математике
Матрица — это таблица элементов, которая состоит из строк (m) и столбцов (n).
Может иметь разные размеры и формы в зависимости от количества находящихся в ней элементов. Элементы фиксированы: если переставить хотя бы один, то получится иная матрица с иными свойствами.
Откуда они взялись, чем полезны
Первые упоминания найдены еще в Древнем Китае, однако широкую известность матрицы приобрели только в середине XVIII, аккурат после выхода книги «Введение в анализ алгебраических кривых» Габриэля Крамера. В своей работе знаменитый математик описал совершенно новый способ решения систем линейных уравнений, который прозвали «методом волшебных квадратов». Сам термин «матрица» появился лишь в XIX веке благодаря трудам английского математика Д.Д. Сильвестра.
В современном мире матрицы используют повсюду. Телефонные справочники, табели успеваемости, отчеты и счета тоже являются матричными моделями. Они полезны, так как имеют прикладное значение.
Применение матриц в математико-экономическом моделировании
В математико-экономическом моделировании матрицы считаются самым удобным способом хранения различных структурированных данных и решения задач с ними. Приведем простой пример из экономической модели «затраты-выпуск».
Дана таблица распределения ресурсов по различным отраслям:
Так, элемент а23 = 5,8 обозначает то, сколько водных ресурсов потребляется в торговле, а элемент а11 = 4,8 обозначает, сколько трудовых ресурсов потребляется в промышленности.
Данная матрица может использоваться при сравнении и оценке востребованности ресурсов в различных отраслях экономики, решении экономических задач предприятий и организаций, анализе затраченных средств в ходе производства.
Видео
Словарь Ефремовой
матрицаж. Углубленная металлическая форма, применяемая при штамповке металла, при отливке типографских литер и т.п. Обратная углубленная копия, снимаемая с набора на картоне, свинце, пластмассе и т.п., для отливки стереотипов, с которых производится печатание. Система каких-л. математических величин, расположенных в виде прямоугольной схемы.
Специальные виды матриц
Нулевая матрица — это матрица произвольного порядка называется нулевой матрицей тогда и только тогда, когда каждый элемент матрицы равен нулю. $ \left( \begin{array}{rrr} 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{array}\right) $
Матрица «вектор-строка» — это матрица, которая имеет только одну строку. $ \left( \begin{array}{rrr} 3x & 2y & 45xy & 9 \end{array}\right) $
Матрица «вектор-столбец» — это матрица, которая имеет только один столбец. $ \left( \begin{array}{ccc} 45 \\ 3 \\ 0 \end{array}\right) $
Энциклопедический словарь
матрица(нем. Matrize, от лат. matrix — матка), в полиграфии — 1) металлическая пластинка с углубленным прямым изображением буквы или знака, изготовленная штамповкой пуансоном или гравированием. Служит формой для отливки литер в шрифтолитейном и наборном производствах. 2) Лист пластичного материала с углубленным изображением текста и рисунков, полученный прессованием с оригинальной формы высокой печати. Применяют при изготовлении стереотипов; хранится вместо набора (для целей переиздания, децентрализации печатания многотиражных изданий). 3) Рельефная копия штампа (контр-штамп), используемая при конгревном тиснении.в металлообработке — инструмент со сквозным отверстием (реже углублением), используемый при штамповке, прессовании и волочении для выдавливания, свертки или протягивания заготовки.в математике — прямоугольная таблица каких-либо элементов aik (чисел, математических выражений), состоящая из m строк и n столбцов: Если m=n, то матрица называется квадратной. Над матрицей можно производить действия по правилам матричной алгебры. Матрицы используются во многих разделах математики и физики, в частности при исследовании систем m линейных уравнений с n неизвестными.
Диагонали матрицы
Диагональ матрицы, с совпадающими индексами элементов, при условии равенства ее строк и столбцов, называют главной диагональю матрицы.
Например, в матрице

главная диагональ содержит элементы  ,
,  ,
,  ,
,  .
.
Диагональ, которая содержит элементы  ,
,  , …
, …  называется побочной диагональю матрицы. В матрице C эта диагональ представлена элементами
называется побочной диагональю матрицы. В матрице C эта диагональ представлена элементами  ,
,  ,
, 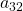 ,
,  .
.
Обозначение
Матрица — это таблица данных, которая берется в круглые скобки:
| A = | 4 | 1 | -7 | ||
| -1 | 2 |
Матрица обычно обозначаются заглавными буквами латинского алфавитв. Матрица содержащая n строк и m столбцов, называется матрицей размера n×m. При необходимости размер матрицы записывается следующим образом: An×m.
Сложение и вычитание матриц
Если в нескольких матрицах совпадает число строк и столбцов, то мы можем их складывать и вычитать. Для вычислений нам нужно поэлементно сложить или вычесть каждый элемент матриц: первый элемент первой матрицы складываем с первым элементом второй матрицы или вычитаем из него и так далее. В результате получаем новую матрицу.


В словаре Д.Н. Ушакова
МА́ТРИЦА, матрицы, ·жен. (·нем. Matrize) (тех.).1. Пластинка с выдавленными, вырезанными обратными знаками или изображениями чего-нибудь, служащая формой для отливки или штамповки. С матриц отливают типографские литеры. Матрицы употребляются при чеканке монеты.2. Бумажная форма, являющаяся обратной копией набора и служащая для отливки стереотипа (·тип. ). Печатать что-нибудь с матриц.
