Что такое ускорение?

Кинематика точки

Вектор ускорения материальной точки в любой момент времени находится путём дифференцирования вектора скорости материальной точки по времени:

.

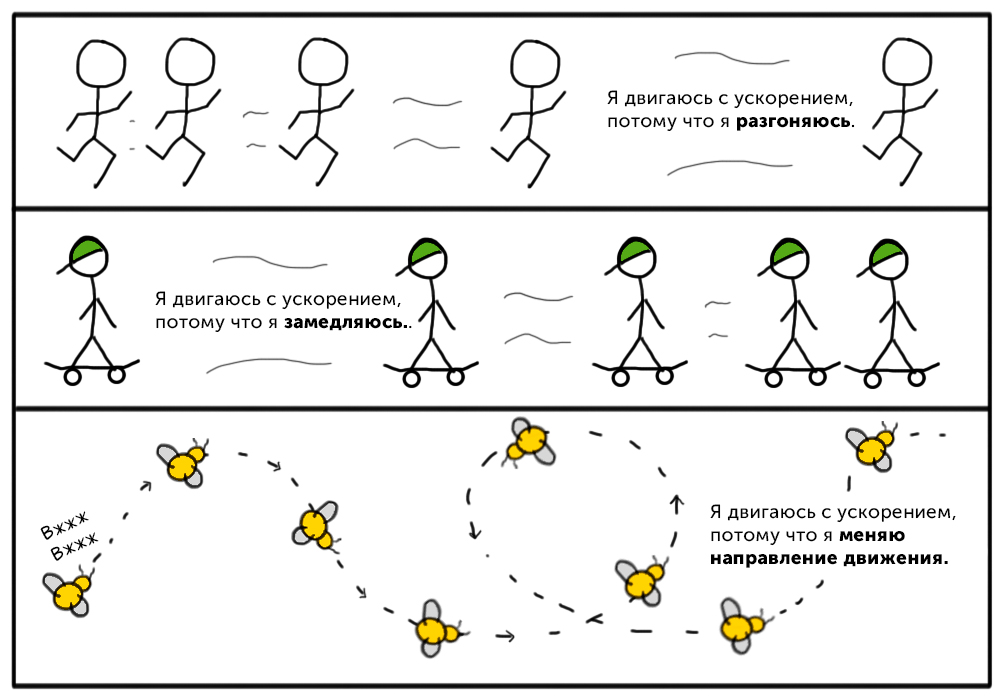
Ускорение точки при прямолинейном движении

Если вектор не меняется со временем, движение называют равноускоренным. При равноускоренном движении справедливы формулы:

.

Частным случаем равноускоренного движения является случай, когда ускорение равно нулю в течение всего времени движения. В этом случае скорость постоянна, а движение происходит по прямолинейной траектории (если скорость тоже равна нулю, то тело покоится), поэтому такое движение называют прямолинейным и равномерным.

Равноускоренное движение точки всегда является плоским, а твёрдого тела — плоскопараллельным (поступательным). (Обратное, вообще говоря, не верно)

Ускорение точки при движении по окружности

w = w_τ + w_n

Тангенциальное ускорение — направлено по касательной к траектории, обозначается w_τ (a_τ). Является составляющей вектора ускорения a. Характеризует изменение скорости по модулю.

Центростремительное или Нормальное ускорение — возникает при движении точки по окружности, обозначается w_n. Является составляющей вектора ускорения w. Вектор нормального ускорения всегда направлен к центру окружности, а модуль равен:

Угловое ускорение — показывает, на сколько изменилась угловая скорость за единицу времени, и, по аналогии с линейным ускорением, равно:

Направление вектора здесь показывает, увеличивается или уменьшается модуль скорости. Если векторы углового ускорения и скорости сонаправлены, значение скорости растёт, и наоборот.

Ускорение точки при движении по кривой

Вектор ускорения можно разложить по сопутствующему базису :

,

где

• — величина скорости,
• — единичный касательный к траектории вектор, направленный вдоль скорости (касательный орт),
• — орт нормали к траектории,
• — орт бинормали к траектории,
• — радиус кривизны траектории.

Известно, что , называемое бинормальным ускорением, всегда равно нулю.

Векторы и 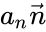называются касательным (тангенциальным) и нормальным ускорениями соответственно.

Видео

Единица измерения

Ускорение рассчитывается путём деления метров в секунду (м/с) на секунды (с). Деление расстояния по времени вдвое равно делению расстояния на квадрат времени. Таким образом, единицей ускорения СИ является метр в секунду в квадрате (м/с²). Чтобы было весело изучать физику, можно рассмотреть несколько интересных примеров в таблице.

ᾱ ( м/с²)	Событие
0,5	гидравлический лифт
0,63	ускорение свободного падения (УСП) на Плутоне
1	лифт на кабеле
1,6	ускорение свободного падения на Луне
8,8	Международная космическая станция
10—40	механический прямолинейный старт пилотируемой ракеты
20	космический челнок
9,8	УСП на Земле
20—50	американские горки
80	предел устойчивой человеческой терпимости
0—150	тренировочная центрифуга
600	автоматические подушки безопасности
1 млн	пуля в стволе пистолета
24,8	УСП на Юпитере

Другая часто используемая единица — ускорение силы тяжести g. Поскольку все знакомы с влиянием гравитации на физические объекты, это делает их удобным стандартом для сравнения ускорений. Все чувствуют себя нормально при 1 g, вдвое тяжелее при 2 g и невесомо при 0 g. Эта единица измерения имеет значение 9,80665 м/с², но для повседневного использования достаточно 9,8 м/с², а 10 м/с² удобно для быстрых подсчётов.

Как рассчитать ускорение: формулы

Для прямолинейного движения

Прямолинейное движение — механическое движение, при котором траектория тела — прямая линия.

В этом случае ускорение находится по следующим формулам:

\(a\;=\;\frac{\mathrm V}t\)

\(a\;=\;\frac{2S}{t^2}\)

\(a\;=\;\frac{V^2}{2S}\)

Где \(a\) — достигнутое ускорение тела, \(S\) — пройденный путь (расстояние), \(t\) — затраченное время.

Время отсчитывается от начала движения тела.

При прямолинейном равномерном движении ускорение по модулю равняется нулю.

Для равноускоренного движения

Равноускоренное движение — прямолинейное движение с постоянным положительным ускорением (разгон).

При таком виде движения ускорение определяется по формуле: \(a\;=\;\frac{V-V_0}t\), где \(V_0\) и \(V\) начальная и конечная скорости соответственно, \(a\) — достигнутое ускорение тела, \(t\) — затраченное время.

Для равнозамедленного движения

Равнозамедленное движение — прямолинейное движение с постоянным отрицательным ускорением (замедление).

При таком виде движения ускорение находим по формуле: \(a\;=-\;\frac{V-V_0}t\), где V и V начальная и конечная скорости соответственно, a — достигнутое ускорение тела, t — затраченное время.

Нахождение ускорения через массу и силу

Принцип инерции Галилея:

Если не действовать на тело, то его скорость не будет меняться.

Система отсчета (СО) — система координат, точка отсчета и указание начала отсчета времени.

Инерциальная система отсчета (ИСО) — это СО, в которой наблюдается движение по инерции (соблюдается принцип инерции).

II закон Ньютона:

В инерциальных системах отсчёта ускорение, приобретаемое материальной точкой, прямо пропорционально вызывающей его силе, совпадает с ней по направлению и обратно пропорционально массе материальной точки.

или

\(\overrightarrow a=\frac{\overrightarrow F}m\)

Тангенциальное и нормальное ускорение

Если записать скорость как \( \vec v = v\hat \tau \), где \( \hat \tau \) — орт касательной к траектории движения, то (в двухмерной системе координат):

\( \vec a = \dfrac {d(v\hat \tau)} {dt} = \)

\( = \dfrac {dv} {dt} \hat \tau + \dfrac {d\hat \tau} {dt} v =\)

\( = \dfrac {dv} {dt} \hat \tau + \dfrac {d(\cos\theta\vec i + sin\theta \vec j)} {dt} v =\)

\( = \dfrac {dv} {dt} \hat \tau + (-sin\theta \dfrac {d\theta} {dt} \vec i + cos\theta \dfrac {d\theta} {dt} \vec j)) v \)

\( = \dfrac {dv} {dt} \hat \tau + \dfrac {d\theta} {dt} v \hat n \),

где \( \theta \) — угол между вектором скорости и осью абсцисс; \( \hat n \) — орт перпендикуляра к скорости.

Таким образом,

\( \vec a = \vec a_{\tau} + \vec a_n \),

где \( \vec a_{\tau} = \dfrac {dv} {dt} \hat \tau \) — тангенциальное ускорение, \( \vec a_n = \dfrac {d\theta} {dt} v \hat n \) — нормальное ускорение.

Учитывая, что вектор скорости направлен по касательной к траектории движения, то \( \hat n \) — это орт нормали к траектории движения, который направлен к центру кривизны траектории. Таким образом, нормальное ускорение направлено к центру кривизны траектории, в то время как тангенциальное — по касательной к ней. Тангенциальное ускорение характеризует скорость изменения величины скорости, в то время как нормальное характеризует скорость изменения ее направления.

Движение по криволинейной траектории в каждый момент времени можно представить как вращение вокруг центра кривизны траектории с угловой скоростью \( \omega = \dfrac v r \), где r — радиус кривизны траектории. В таком случае

\( a_{n} = \omega v = {\omega}^2 r = \dfrac {v^2} r \)

Скорость и ускорение

Средняя скорость – векторная физическая величина, равная отношению вектора перемещения к промежутку времени, за которое оно произошло

А теперь представим, что промежуток времени уменьшается, уменьшается, и становится совсем коротким, стремится к нулю. В таком случае о средней скорости говорить на приходится, скорость становится мгновенной. Те, кто помнит основы математического анализа, тут же поймут, что в дальнейшем нам не обойтись без производной.

Мгновенная скорость – векторная физическая величина, равная производной  от радиус вектора по времени. Мгновенная скорость всегда направлена по касательной к траектории.

В системе СИ скорость измеряется в метрах в секунду

Если тело движется не равномерно и прямолинейно, то у него есть не только скорость, но и ускорение.

Ускорение (или мгновенное ускорение) – векторная физическая величина, вторая производная от радиус-вектора по времени, и, соответственно, первая производная от мгновенной скорости

Ускорение показывает, как быстро изменяется скорость тела. В случае прямолинейного движения, направления векторов скорости и ускорения совпадают. В случае же криволинейного движения, вектор ускорения можно разложить на две составляющие: ускорение тангенциальное, и ускорение нормальное.

Тангенциальное ускорение показывает, как быстро изменяется скорость тела по модулю и направлено по касательной к траектории

Нормальное же ускорение характеризует быстроту изменения скорости по направлению. Векторы нормального и тангенциального ускорения взаимно перпендикулярны, а вектор нормального ускорения направлен к центру окружности, по которой движется точка.

Здесь R – радиус окружности, по которой движется тело.

Нормальное и тангенциальное ускорения

Рассматривая движение материальной точки по криволинейной траектории, удобно вектор полного ускорения разложить на две взаимно перпендикулярных компоненты: $a_{\tau }$aτ​ –тангенциальное и $a_n$an​ –нормальное ускорение:

Вектор тангенциального ускорения имеет направление вдоль касательной, а нормальное ускорение — вдоль нормали к траектории. Модуль тангенциального ускорения является первой производной по времени от модуля скорости:

Модуль нормального ускорения зависит от радиуса кривизны траектории в данной точке траектории и модуля скорости:

$\mid {\vec{a}}_{\tau }\mid =a_{\tau }=\dot{v}$∣aτ​∣=aτ​=v˙

Вектор полного ускорения является векторной суммой тангенциального и нормального ускорений:

$\vec{a}={\vec{a}}_{\tau }+{\vec{a}}_n$a=aτ​+an​

Модуль полного ускорения находят по теореме Пифагора:

$a=\mid \vec{a}\mid =\sqrt{a_{\tau }^2+a_n^2}=\sqrt{{\dot{v}}^2+\frac{v^4}{R^2}}$a=∣a∣=aτ2​+an2​​=v˙2+R2v4​​

Движение точки называется ускоренным, если численное значение ее скорости увеличивается со временем, то есть $а>$а> движение точки называется замедленным, если численное значение ее скорости уменьшается со временем, то есть а<. Если $a_{\tau }=$aτ​=, то материальная точка совершает равномерное движение, а если $a_n=$an​= – движение по прямой (прямолинейное движение). Величины $a_{\tau }$aτ​ и $a_n$an​ характиризуют скорость изменения в соответствии с численным значением и направлением скорости движущейся материальной точки.

Теги